This short essay gives a brief introduction to F-theory and assumes some basic knowledge of string string—therefore you may want to read the text on string theory first.
What is F-theory?
If one picks a particular variant of the 10d perturbative string theory, the Type-IIB superstring, the theory comes with two naturally defined scalar fields, one being the dilaton (which is related to the string coupling) and the other one being the axion (the C0 Ramond-Ramond field). Putting together both values this gives rise to a single complex scalar field, appropriately called the axio-dilaton. Due to a certain symmetry that merges and transforms the two fields into each other, the axio-dilaton can be interpreted as the so-called modulus of 2-torus—the shape of a donut. Historically, this geometric reinterpretation of the so-called Type-IIB S-duality symmetry, which relates the strong coupling regime to the weak coupling regime, was the foundation of F-theory. However, the actual meaning of the letter “F” as chosen by Vafa1 in 1996 remains a well-kept mystery much like the infamous “M” in Witten’s M-theory.

As the values of the two original fields—the axion and dilaton—and the associated axio-dilaton are varying for each point of the 10d space-time, the geometry of the associated 2-torus (like its thickness) is varying as well. In a more mathematical language, one can describe the total space of this construction (i.e. the association of a particular 2-torus to each point of the base space) as an elliptically-fibered bundle, which is 12-dimensional (10d base and 2d torus). Like in ordinary string theory models, 4 dimensions of the base are assumed to be flat, corresponding to our everyday experience of three spatial and one temporal dimension. Therefore an 8-dimensional part of the 12d total space is actually non-trivial and considered to be the internal geometry of the model. Due to various phenomenological conditions like supersymmetry and general stability, the internal 8d space has actually to be a Calabi-Yau 4-fold, a very specific kind of mathematical space. Remember that it has to be elliptically-fibered as well. Regarding the original question, F-theory is actually the theory living on this 12-dimensional total space, and is treated as a non-perturbative completion of the underlying 10d Type-IIB string theory. Via a chain dualities F-theory can indirectly be formulated in terms of M-theory, and another duality connects it to the heterotic string theory. However, properly showing how this all works out in detail is an extremely lengthy task and unfortunately there is not even a good textbook on the subject.
F-theory basically is a geometric reinterpretation of a certain duality of the IIB superstring theory, where contact with the everyday 4-dimensional world is established by compactifying on a elliptically-fibered Calabi-Yau 4-fold internal geometry. Neat!
The interesting part of F-theory is that the elliptic fibre—the torus—can degenerate, i.e. it can become a circle, shrink to a point or whatever other monstrosities one can create from a donut. But as its geometry is related to the dilaton field, which in turn is related to the string coupling, such degenerations of the elliptic fibre are therefore associated with “strong coupling” regions of the underlying theory. By working out the corresponding mathematics properly, it turns out that those parts of the base space where the attached fibre degenerates can be identified with the position of 7-branes. Furthermore, as the fibre can degenerate in many different ways—which leads to singularities not only in the elliptic fibre but potentially also in the Calabi-Yau 4-fold itself—one can in fact associate a specific gauge group of higher rank to such a 7-brane. Therefore, the F-theory 7-brane differ from the ordinary D7-branes one expects from Type-IIB string theory, and the direct identification between the two is not as straightforward as one might exect. For example, in the F-theory framework without much effort one encounters high-rank gauge groups like the exceptional groups \(E_6\), \(E_7\) or \(E_8\) which are never obtained in the perturbative IIB theory. In other cases the F-theory 7-brane is actually identified with an O7-plane, which is a fixpoint set of some space-time symmetry in the IIB string theory. Later the origin of the exceptional groups could be understood in terms of string networks between the branes, which requires taking the aforementioned S-duality symmetry fully into account.
One great benefit of the F-theory approach is therefore that one can naturally get many different objects from the unified concept of geometric singularities which are either absent in the perturbative Type-IIB theory or have to be placed in artificially by hand. This is partially due to the intrinsically non-perturbative nature of F-theory.
- 1996: Vafa’s original paper “Evidence for F-theory”
- 1996: Important paper on geometric singularities and gauge symmetry
- 1998: Exceptional gauge groups via (p,q)-string networks: part 1 and part 2
- 2008: Denef’s lectures on IIB model building with a significant focus on F-theory
F-theory model building
Local models
Unfortunately, there is also a rather huge drawback: Remember that the F-theory actually has to be defined on an elliptically-fibered Calabi-Yau 4-fold to make even remotely sense. This is a mathematically extremely restrictive condition, in particular if one also wants to have some specific configuration of 7-branes (which is directly encoded into the degenerations of the elliptic fibre and therefore into the 4-fold geometry itself). Satisfying all those constraints at the same time is a rather hard task, and there are also many further phenomenological constraints imposed from well-established experimental data.
As a first step one may therefore consider local models: One essentially selects one of the 7-branes and considers then the effective 8d worldvolume gauge theory on just this particular 7-brane, which becomes non-trivial due to potential brane intersections. This requires the geometry of the particular 7-brane to be shrinkable, which effectively allows to decouple the local physics from the rest of the dynamical constituents of the full theory. In a generic setting, all the branes are strongly interacting with each other and may recombine or align / form a stack—therefore the requirement of this “decoupling principle” places once again further restrictions on the geometry. However, assuming that those conditions are all satisfied, the 8d local physics is only concerned about the intersections of this brane with all the others present in the considered geometry. Essentially, one forgets about the complicated Calabi-Yau geometry and just sits on one of the branes. In most cases a 7-brane which carries a simple GUT group like \(SU(5)\) or \(SO(10)\) is selected for the decoupling.
The decoupling principle allows to work with some of the elegant features of the F-theory framework without having to work out all the details of the entire Calabi-Yau 4-fold geometry. It is also motivated from the more general perspective that (as a naturality condition) the physics localized in some small region of the internal manifold is not too much affected by the entire global structure. This is more generally called the local string model building approach and has its roots in the locality paradigm, which is found in quantum field theories as well. The appreciation of the fact that F-theory allows for exceptional gauge groups together with the decoupling approach stirred a sort of second wave of interest beginning in 2008 for the F-theory model building approach, which was more or less neglected and forgotten in the late ’90s. Intersecting 7-branes
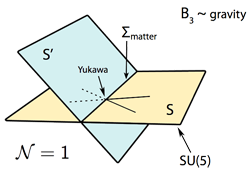
One can now ask what happens if two 7-branes intersect. Since without further notice 7-branes (like all other p-branes) are assumed to be filling out the 4 flat space-time dimensions, 4 of the 8 dimensions of a 7-brane worldvolume are effectively irrelevant—we are considering the 4 remaining dimensions inside the 6d internal base of the Calabi-Yau 4-fold with their respective positions encoded in the degeneration of the elliptic fiber. Therefore, we are left with two intersecting complex 2d planes. Unless both are perfectly aligned (i.e. coincident), this setting generically leads to an intersection curve. Along this intersection curve, the degeneration of the elliptic fibre is much worse compared to the individual 7-branes, i.e. one encounters a singularity enhancement. Ultimately after properly working out the technicalities it becomes clear that the physical states localized on those intersection curves actually give rise to (chiral) matter—thus they are usually called “matter curves” in this context.
Likewise, one can also consider what happens when three 7-branes intersect in a single point. In fact—and this is actually quite surprising considering the geometry—it turns out that in a single point usually four 7-branes are intersecting. From the perspective of the selected and decoupled GUT 7-brane this means that there are actually three matter curves intersecting, which gives rise to a Yukawa coupling between the respective matter states. Alltogether, one can neatly encode the GUT gauge group, the matter types and the Yukawa couplings into a configuration of intersecting 7-branes, which in the F-theory approach is entirely encoded into the geometry of the Calabi-Yau 4-fold and its elliptic fibration. A rather beautiful geometric picture from the theoretical point of view!

Going global
However, there is only so much one can do from the local point of view. While the local model approach is great to analyze some different kinds of couplings and phenomenological properties arising from certain 7-brane configurations, ultimately there are certain consistency conditions which can only be checked in a global model. For a generic setting which looks perfectly fine in the local context, the existence of a “global” Calabi-Yau 4-fold which contains the same 7-brane configuration with all intersections etc. is by no means guaranteed. Certain global conditions like charge and tadpole cancellation may require the introduction of further 7-branes, which in turn may ruin the phenomenology of the precisely hand-crafted local model. Therefore, the “big issue” in F-theory model building is to find global models.
One has to put this statement into perspective to the situation in Type-IIB theory, where the story actually began: In Type-IIB string theory one starts with a fixed background geometry and just plugs in the branes to one’s liking, provided they satisfy some rather simple consistency conditions. In F-theory on the other hand, “plugging in the 7-branes” means actually finding a suitabe elliptically-fibered Calabi-Yau 4-fold—there is no simple “plugging in” as the entire internal geometry is affected. Ultimately, this is once again due to the non-perturbative nature of F-theory, which so to speak also takes the backreactions of the branes on the space-time geometry into account.
Handling Calabi-Yau geometries is really tricky. For example, there is not a single explicit metric known for ANY compact Calabi-Yau 3- or 4-fold. One only has indirect access to the geometry by the means of its topological properties (for example, the Calabi-Yau condition can be restated as the vanishing of the first Chern class of the tangent bundle). However, using toric geometry—a branch of (projective) algebraic geometry—a certain level of geometric engineering of Calabi-Yau 4-folds is gained. For example, in a weighted projective space any hypersurface which is of the order of the sum of all the weights actually has vanishing first Chern class, i.e. gives a Calabi-Yau geometry. From a basic viewpoint toric geometry is the natural generalization of (weighted) projective spaces, allowing to assign multiple projective weights to each coordinate and corresponding conditions in those different weight systems. Toric spaces can also be neatly described in terms of a so-called fan, which is basically a collection of cones made from a set of lattice vectors.
Therefore, at the moment all considered Calabi-Yau 4-fold geometries ultimately originate from toric settings and the aforementioned phenomenological consistency conditions have to be appropriately translated and imposed in the language of toric geometry. The complexity of this task makes an exhaustive search very difficult. Model building:
- 2008: The exceptional brane papers: part 1 and part 2
- 2009: First global model with three chiral matter generations
- 2010: A summary of phenomenological implications
And the future?
Slowly but steadily many different pieces of the F-theory approach puzzle come together. However, the ultimate goal of obtaining a phenomenologically realistic model remains rather elusive at this stage. In fact, more and more results indicate that satisfying all the phenomenological conditions (besides the aforementioned generic geometrical constraints which of course have to be met as well) in a global model becomes an increasingly more difficult task to handle. For example, in a paper by the Caltech group one is led to a tradeoff result while attempting to solve a great number of constraints, where ultimately one can only chose between one phenomenological desaster and the other. But one has to remember the numerous restrictions and assumptions that took place in order to reach this point. By no means provides toric geometry an exhaustive treatment of all Calabi-Yau 3- or 4-folds, so if further work actually proves that there are no “good ones” in those approaches they may very well lie outside the toric regime. From a more optimistic point of view, one may view the apparently over-constraining conditions arising from the F-theory GUT approach to be somewhat predictive, as it seems to leave little room for fine-tuning. The great variety of F-theory models quickly dwindles away as soon as phenomenological constraints are posed.
Obviously, much more effort has yet to be put into this particular are of string theory…
-
See Vafa’s original paper “Evidence for F-theory” from 1996. ↩